Regressionsanalyse

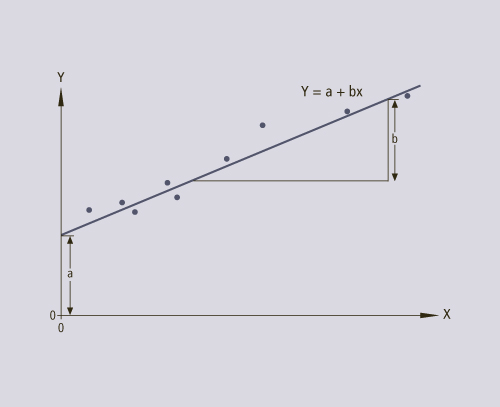
Verfahren der Datenanalyse. Hierbei wird die Art des Zusammenhangs zwischen Variablen und der Möglichkeit ihrer funktionalen Beschreibung durch statistische Analyse der Abhängigkeit einer Zielvariablen (Kriteriumsvariable) und einer oder mehrerer erklärenden Variablen (Prädiktorvariablen) untersucht. Das Prinzip aller Verfahren der Regressionsanalyse besteht in der möglichst genauen Anpassung einer theoretischen Funktion an die empirischen Wertepaare, wie sie in einem Streudiagramm dargestellt werden können (Abbildung R-9).

Als Verfahren zur Berechnung der Regressionsgerade wird meist die Methode der kleinsten Quadrate angewendet, bei der die Parameter der Regressionsgerade so bestimmt werden, dass die Summe der quadrierten Abstände zwischen den empirischen Werten und der Regressionsgerade minimiert wird.

Zu unterscheiden sind folgende Analysearten:

1. Lineare Einfachregression, bei der von einer linearen Beziehung zwischen einer unabhängigen (X) und einer abhängigen Variablen (Y) ausgegangen wird:

   Y = a + b × X

2. Lineare Mehrfachregression, bei der eine lineare Beziehung zwischen mehreren unabhängigen Variablen (Y¹, Y²,…,Yⁿ) und einer abhängigen Variablen unterstellt wird:

   Y = a + b¹ × X¹ + b² × X² +… + bⁿ × Xⁿ

3. Nichtlineare Einfachregression, bei der der funktionale Zusammenhang zwischen unabhängiger Variable (X) und abhängiger Variable (Y) nichtlinear ist:

   Y = a × X^b
   

4. Nichtlineare Mehrfachregression, bei der von einem nichtlinearen Zusammenhang zwischen den unabhängigen Variablen (X¹, X²,…,Xⁿ) und der abhängigen Variablen (Y) ausgegangen wird:

   z. B. Y = a + b¹ × X¹ + b² × X^{2 2}

Zur Anwendung kann die Regressionsanalyse z. B. bei der Ermittlung einer → Preis-Absatz-Funktion kommen.